DC Tesla Coil design

DC RESONANT CHARGING CIRCUIT

Instead of charging the capacitor through a series resistor, there is much to gain by using an inductor to control the charging characteristics. This section explains how the tank capacitor can be charged through a suitably chosen inductor. The operation of a simple DC resonant charging circuit is explained first, then the section goes on to discuss the benefits of including a blocking or "de-Q-ing" diode. Finally, the section concludes with some design equations and a list of advantages and disadvantages of the DC resonant charging scheme.

The circuit below represents the simplest DC resonant charging arrangement.

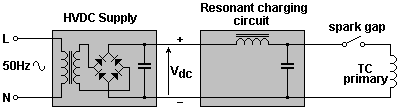
An inductor has the following properties which make it very useful in a DC charging circuit meant for Tesla Coil use:-

Low impedance at DC.
An ideal inductor presents zero resistance to the flow of Direct Current. Therefore it does not interfere with the charging of the tank capacitor from the DC source.
High impedance at high frequency.
The inductor presents a very high resistance to the flow of high frequency current. This effectively "isolates" the tank capacitor from the charging circuit when the spark gap fires and the primary oscillates at several hundred kHz. Loading is minimised and primary Q is preserved.
It is lossless.
An ideal inductor has no losses, therefore it cannot waste power by dissipation as heat. (Real inductors have some winding resistance, so dissipate a small amount of power in the form of heat.)
Current cannot change instantly.
An inductor does not allow instantaneous changes in the current passing through it. This means that the brief firing of the spark gap does not instantly short-circuit the HVDC supply. This property of the inductor also determines how quickly the tank capacitor charges from the DC supply after each bang.

Operation of the DC resonant charging circuit

The DC resonant charging circuit is merely a series resonant LC circuit connected across a DC supply. The "frequency domain" behaviour of this type of circuit is very familiar to us, with its resonant peak at Fres, etc. However, here we are interested in how it behaves with time. It is the "transient response" which tells us how the capacitor charges from the HVDC supply over time...

Initially the tank capacitor is "empty" and has no voltage across it. The full DC supply voltage is developed across the charging inductor. No current flows around the circuit at this time.
The voltage across the charging inductor means that current gradually starts to flow through the inductor. The current actually rises at a rate determined by the inductance of the charging reactor. As this current flows it charges up the tank capacitor. The current flowing in the inductor implies that energy is stored already in the magnetic field of this component. Remember E = 0.5 I² L
Eventually the capacitor charges up to the point where its voltage equals that of the DC supply. At this instant there is no voltage across the charging inductor, and maximum current is flowing. Although there is no voltage across the charging inductor at this time, the current through an inductor cannot change instantaneously. The inductance of the charging reactor acts like a flywheel and keeps the current flowing in the same direction ! As the magnetic field in the inductor collapses, it realeases the energy that it stored earlier in the charging cycle. It effectively becomes another power source.
Since the charging inductor is in series with the DC supply, its inductive kick (or EMF) adds to that of the DC supply. Therefore the capacitor is charged to a voltage higher than the DC supply alone could achieve. Eventually the magnetic field in the inductor has decayed completely, and all of its stored energy has been transfered to the tank capacitor. At this time the capacitor voltage is TWICE the DC supply voltage, and the charging current falls to zero. Now is a good time to fire the spark gap since the tank capacitor is at its maximum voltage.
The whole trick is firing the spark gap at the right time. If the spark gap is not fired when the tank capacitor is at its maximum voltage this is what happens... The tank capacitor has been charged to a voltage higher than the DC source, therefore a voltage exists across the charging inductor. (This time the inductor voltage is of the opposite polarity.) Current begins to flow in the opposite direction, from the tank capacitor through the inductor back to the DC source. Essentially the tank capacitor is transfering some of its stored energy back to the charging reactor ! This resonant exchange of energy between inductor and capacitor continues until the spark gap fires removing some energy from the system.
When the spark gap fires, the tank capacitor is instantly emptied of its stored charge and its terminal voltage returns to zero. Now the full supply voltage appears across the charging inductor and the whole process starts again from the beginning.

The graph below shows the exact inductor current waveform and the capacitor voltage waveform.

Notice the "half-sine" shape of the charging current, and how the inductor current returns to zero for each firing of the rotary spark gap.

Also notice the sinusoidal charing profile of the capacitor voltage. It starts to charge slowly at first. Then charges faster as the inductor current increases, and finally slows down again as it approaches twice the DC supply voltage.

The inductor current is actually proportional to the derivative (or gradient) of the capacitor voltage. This is to be expected since the capacitor "integrates" charge that is passed to it. Knowing this information it is easier to understand why the waveforms have these shapes.

The inductance of the charging reactor has controlled the rate at which our tank capacitor charged from the DC supply in a similar way to charging through a series resistor. However the inductor stores and releases energy that the series resistor wastes as heat. Where the resistive charging circuit is only 50% efficient due to power dissipation in the early part of the charging cycle, the inductive charging circuit stores this energy and uses it to charge the capacitor to twice the voltage. Current limiting and voltage doubling at the same time !

It is also highly desirable that the charging current falls to zero around the time that the spark gap is meant to fire. This greatly reduces the likelihood of power arcing or "trailing arcs" in the rotary spark gap due to a high DC current.

In the case of the resistive charging circuit, we saw that the highest charging rate occurred immediately after the spark gap had fired and discharged the tank capacitor. We also discussed how this rapid rate of charge could quickly return the capacitor to sufficient voltage to re-ignite the spark in the rotary gap if the hot electrodes had not adequately separated. This can be contrasted to the slow rate of charging found immediately after each firing in the resonant charging case. This more gradual start to the charging cycle helps to prevent re-ignition of the spark gap before the electrodes have had time to move far apart.

The "Weight on a spring" model

I think that the operation of the DC resonant charging circuit can be best understood by way of a mechanical analogy. Consider a weight hanging by a spring from the edge of a table. It is clear that a weight hanging from a spring is a mechanical resonant system and has its own natural resonant frequency. If you pull the weight down from its resting position and release it, the weight will oscillate around its resting position at some frequency. We will see that this very closely models the behaviour of our LC resonant charging circuit...

The level of the table represents the fixed HVDC supply voltage. The height of the weight above ground represents the voltage across the tank capacitor. The hand pulling the weight down to ground level represents the action of the spark gap, periodically discharging the tank capacitor.

Initially the tank capacitor is fully discharged. This is represented by the weight being held at ground level.

The full supply voltage is developed across the charging inductor, represented by considerable tension in the spring.

When the weight is released it accelerates towards the level of the table from which it is hanging. This represents the capacitor charging up to the HVDC supply voltage through the inductor.

When the weight reaches the level of the table, it has considerable momentum and continues to move upwards beyond the table from which it is hanging. This momentum is akin to the magnetic energy stored in the charging inductor at this instant.

Since the weight is now above the spring, it decelerates and momentarily stops at its highest point.

This swinging of the weight above the level from which it is supported closely models the way in which the tank capacitor charges to a voltage in excess of the HVDC supply. It is due to the "momentum" of current flowing in the charging inductor.

The point at which the weight comes to rest is marked by a red arrow in the animation above. This is the maximum voltage that the capacitor reaches, and is equal to TWICE THE HVDC SUPPLY VOLTAGE. This is the optimum time to fire the spark gap.

Following this point, the capacitor voltage begins to fall. It ultimately oscillates about the HVDC rail at the resonant charging frequency for many cycles, just as our weight would continue to bounce up and down after being disturbed.

When the spark gap fires, it discharges the capacitor back to zero volts, and the resonant charging cycle begins again. This is represented by a hand pulling the weight back to ground level and then releasing it.

I think that this mechanical analogy is very useful in "getting your head around" what is happening in a resonant charging circuit. Many of the properties of the DC resonant charging circuit can be explained by referring back to this model.

Extinction frequencies

From the animated model above, we saw that the best time to fire the spark gap was when the capacitor voltage was at its maximum value. This occurs after the capacitor has been free to charge for half of the resonant period of the charging circuit. i.e. The optimum firing rate for a rotary spark gap is equal to twice the resonant frequency of the charging circuit. Firing at any other time will give less than maximum power throughput.

However, we also discussed how the capacitor voltage continues to oscillate freely about the HVDC supply voltage, and returns to zero volts at regular intervals. It is clear that any attempt to fire the spark gap when the capacitor voltage is near zero volts will process little power ! These points are marked by RED arrows.

We can quickly see that the capacitor voltage returns to zero after every complete period of the resonant charging circuit. Therefore attempting to fire the gap at whole multiples of this period will achieve no power throughput. In fact the firings only serve to reinforce the natural oscillation of the charging circuit, but do not remove any energy from the system.

Any firing rate which is a factor of the resonant charging frequency forces the power throughput to zero. I refer to these firing rates as "extinction frequencies".

Simulations of a typical LC resonant charging circuit reveal that the power throughput rises linearly with rotary BPS except for the deep notches at the extinction frequencies. In this example the charging inductor and tank capacitor were chosen to make the charging circuit resonate at 500Hz. Therefore the extinction frequencies are 500Hz, 250Hz, 167Hz, 125Hz etc...

The RED line shows how the power throughput varies over a wide range of rotary firing rates.

The BLUE line shows the ideal characteristic if the extinction frequencies did not occur.

The graph shows that the behaviour of this DC resonant charging circuit still does not allow complete freedom in the choice of firing rates if the extinction frequencies are to be avoided.

Fortunately, a simple addition to the charging circuit can fix this problem...

De-Q-ing the charging circuit

The extinction frequencies occur because the capacitor voltage returns to zero after reaching its peak value. This occurs because current begins to flow from the tank capacitor back through the charging inductor after the capacitor has reached maximum voltage. We would very much like the capacitor voltage not to fall, and instead remain at its maximum voltage for two reasons. Firstly this ensures maximum power throughput, and secondly we have freedom in our choice of exactly when to fire the spark gap.

This can be achieved by placing a high voltage diode in series with the charging inductor as shown. The diode allows current to flow from left to right through the inductor, charging the capacitor as before. However, it prevents the inductor current from changing direction and halts the resonant process when the capacitor is at twice the supply voltage.

This means that the tank capacitor is always charged to twice the HVDC supply voltage in one half of the resonant charging period. The capacitor is then left in the fully charged state until the spark gap fires. The RED waveform below shows how a capacitor charges to 20kV from a 10kV supply when the de-Q-ing diode is included in the charging circuit.

The top trace shows the current through the charging inductor during the charging cycles.

Notice how the current through the inductor has been at zero for some time before each firing of the spark gap. Also notice how the current builds gradually after the spark gap fires.

The dotted lines depict what would happen if the de-Q-ing diode were not fitted.

Instead of choosing the charging inductor and capacitor values based entirely on the intended rotary firing rate, the designer can now choose values based on the desired charging profile, peak charging current, etc. This is because the natural resonance in the charging circuit has been "killed-off" by the insertion of the diode inside the resonant circuit. Any link between the natural resonant frequency of the charging circuit, and the firing rate of the rotary gap has been removed.

The operator now has freedom in their choice of spark gap firing rate, provided that they allow the minimum time required between firings for the capacitor to complete its charging operation. This permits very slow repetition rates to be evaluated without any extinction frequencies, or high Q-oscillations building up in the charging circuit.

It should be realised that the function of the de-Q-ing diode can be performed by the DC bridge rectifier in 3-phase designs where no HVDC smoothing capacitor is used. The lack of a separate de-Q-ing diode and potentially lethal DC smoothing capacitor make such 3-phase supplies ideally suited to variable speed DC resonant charging.

New Power throughput curve

With the de-Q-ing diode in place the tank capacitor is always charged to twice the DC supply voltage before each firing of the spark gap. This gives a constant bang energy regardless of rotary speed, so the power throughput is now directly proportional to the rotary firing rate. See graph below:

This property of the DC resonant charging circuit is attractive because it allows the power throughput of a large system to be controlled smoothly without requiring a large variac stack or adjustable ballast.

Full supply voltage can be applied to the system with the rotary spark gap running at a low speed to limit the power draw initially.

The rotary speed can then be increased gradually until the required power level is reached.

Maximum rotary speed

The maximum rotary speed is dictated by the time required for the resonant charging circuit to charge the capacitor to twice the supply voltage. The time required is equal to one half of the period of the charging circuit. In other words, the maximum firing frequency of the rotary spark gap should be limited to twice the resonant frequency of the charging circuit if the tank capacitor is to be fully charged.

But what happens if this speed is exceeded ?

The inductor current no longer falls to zero when the spark gap fires. The benefits of zero current at the firing instant are lost. The spark gap now grabs the charging current when it fires, and "arc-trailing" becomes a possibility.

Rather surprisingly the capacitor still charges to 2 x Vdc before each firing ! However it requires many firing cycles to build up sufficient energy in the charging circuit before this is achieved.

Possible saturation of charging inductor due to large DC current component ???

Rotary dwell time

When the rotary electrodes align and the spark gap fires, the HVDC supply is short-circuited except for the charging inductor. It is the charging inductor that limits the current that flows from the HVDC supply through the conducting spark gap. In fact the charging inductor limits the rate at which the DC current from the supply rises when the gap conducts.

When the spark gap fires the charging inductor is connected directly across the HVDC supply. Its current cannot change instantaneously. Instead the current begins to rise at a rate determined by the inductor value and the DC supply voltage across it. The equation V = L di/dt can be rearranged to determine how quickly the DC current will build up:-

di/dt = V / L

For typical values of V and L, the DC current through the inductor might rise at approximately 1000 Amps per second when the spark gap is conducting. At first this sounds very high, but we must remember that the spark gap should only be conducting for a relatively short period of time as the TC primary oscillates.

If the dwell time of the spark gap is only 100us, then the DC current will only have risen to 100mA during the time that the spark is conducting. This figure is relatively small compared to the much larger current caused by the discharge of the tank capacitor into the TC primary coil. Therefore a figure of 100mA is not anticipated to present any problem.

However, we can see that a potential problem arises if either the inductor value is very small, or the conduction time of the rotary spark gap is too long.

In cases where the current rises too quickly, or the dwell time is excessive, the current flow from the HVDC supply may ramp-up to a very high level. Such a level of direct current through the ionised spark channel will heat it to a higher temperature and make it more conductive. Spark gaps normally stop conducting when the AC current goes through zero, but DC current does not cross zero ! This acts to prevent quenching of the arc, allowing the DC current more time to increase even further !

This runaway situation can lead to power arcing or "arc trailing" in the rotary spark gap, as the level of current "follow-through" from the HVDC power supply causes it to resist quenching. The behaviour is similar to the way in which the arc formed by a Jacob's Ladder is stretched out to a great length once it has struck.

This power arcing is very undesirable. It represents considerable current flow from the DC supply which should be going into charging the tank capacitor before the next firing. Instead, this current takes the easier path through the power arc in the rotary gap. This causes considerable energy to be wasted and imposes additional stresses on the HVDC supply, charging inductor and diode. The power arcing quickly erodes the spark gap electrode material and can even lead to chaotic firing of the spark gap.

So how can this problem be avoided ?

In summary the power arcing problem can be reduced by specifying a suitably large charging inductor to limit the rate of rise of current. In addition to this, it is a good idea to use a large rotary disc, with relatively small electrodes fitted to it. This acts to minimise the mechanical dwell time when the electrodes are within sparking distance. However the operator should still avoid running the rotary at very low speeds where the dwell time is massively exaggerated.

Snaking the spark through many gaps in series might help to reduce this problem, as might adding a small resistance in series with the charging choke to limit peak current. It should be realised that the author does not have much experience with this problem, and therefore cannot elaborate further on possible solutions.

DESIGN EQUATIONS

The important variables in the design of a DC resonant charging circuit are the natural resonant frequency of the LC combination, and the characteristic impedance of the charging circuit. The resonant frequency determines the time taken to charge up the tank capactior and the maximum rotary firing rate that should be used. The characteristic impedance determines the power throughput aspects of the design.

Going back to our mechanical analogy, it is relatively easy to grasp what the natural resonant frequency of the charging circuit is, and how it effects the behaviour. We can easily imaging combinations of springs and weights that will oscillate at low frequencies, and other combinations that will oscillate at high frequencies. What is not so intuitive is the meaning of the characteristic impedance. I propose that a circuit with a low characteristic impedance be represented by a thick heavy duty spring and large weight. This implies a lot of stored energy in both components and the ability to process large quantities of power. In contrast a resonant circuit with a high characteristic impedance would be represented by a more delicate spring and a lighter weight. This system may be made to resonate at the same frequency as its more substantial counterpart, but clearly has far less stored energy.

The table below shows some equations that are useful when working with the DC resonant charging arrangement. In particular these equations aid the designer in the choice of the Charging Inductor Lr and the Tank Capacitor Cp.

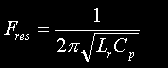	Resonant Frequency of charging circuit. (This is the standard equation for resonant frequency.)	Hertz
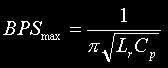	Maximum Rotary firing rate. The maximum BPS is twice the resonant frequency of the charging circuit. This is because the charging operation takes one half cycle at the resonant frequency to complete. Correct resonant charging action no longer takes place above this maximum speed.	Breaks per second
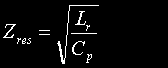	Characteristic impedance of resonant charging circuit. This gives an indication of the loading that the resonant charging circuit presents to the DC supply. It is also used later to calculate the peak charging current.	Ohms
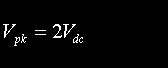	Peak voltage to which tank capacitor charges. The capacitor is charged to twice the DC supply voltage for all rotary speeds below the maximum allowable BPS.	Volts
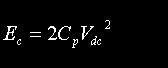	Energy stored in tank capacitor before firing. Obtained by substituting 2Vdc into the familiar energy equation.	Joules
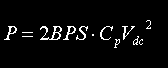	Power throughput at a particular firing rate. Obtained by multiplying the capacitor energy by the rotary firing rate.	Watts
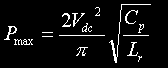	Power throughput achieved at maximum BPS. This is the maximum power throughput that can be achieved by running the rotary at the maximum allowable speed. Obtained by substituting the value for maximum BPS into the power equation above.	Watts
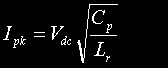	Peak current through the charging inductor. Obtained by dividing the DC supply voltage by the characteristic impedance of the resonant charging circuit. This also represents the peak current drawn from the DC reservoir capacitor during the charging cycle.	Amps
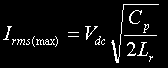	RMS current through charging inductor at maximum rotary BPS. This is the RMS current that the charging inductor will see when the system is run at full power. The charging inductor should be rated appropriately.	Amps
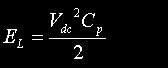	Peak energy stored in the charging inductor during charging cycle. Obtained by substituting the peak inductor current into the familiar inductor energy equation. Notice that the peak inductor energy is independent of the actual inductor value, and it is equal to a quarter of the energy that is finally stored in the tank capacitor !	Joules
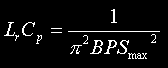	Product of charging inductor and tank capacitor values. Obtained by rearranging the equation for maximum BPS. This is used as a step to derive to the design equations for Cp and Lp below.	-
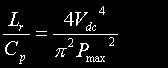	Ratio of charging inductor and tank capacitor values. Obtained by rearranging the equation for maximum power. This is also used as a step to derive the design equations for Cp and Lp below.	-
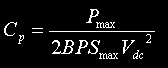	Tank capacitor value for specified power at specified maximum BPS. Use this equation to calculate the capacitor size required to achieve your chosen maximum power at your chosen maximum rotary speed.	Farads
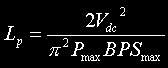	Charging inductor value for specified power at specified maximum BPS. Use this equation to calculate the inductor value required to achieve your chosen maximum power at your chosen maximum rotary speed.	Henries

Note that the last two equations are most important since these are the ones that a designer will employ if designing a DC resonant charging circuit to a specification, from scratch. The other equations can then be used to check peak energies, RMS currents etc.

Design example

Design a DC resonant charging circuit to process a maximum power of 8kW. The highest rotary speed will be 500 BPS, and a 10kV DC supply will be used to power the system. What values of Charging Inductor and Tank Capacitor should be used to meet this specification ?

The inductor value is found by substituting Pmax, BPSmax and Vdc into the last equation to get:

Lp = 5.1 H

The tank capacitor value is found by substituting Pmax, BPSmax and Vdc into the second from last equation to get:

Cp = 80 nF

The RMS current rating required for the charging inductor can now be found by substituting Cp and Lp values into the 9th equation in the table. This gives:

Irms = 886 mA

We know that the peak capacitor voltage will be twice the DC supply voltage. i.e. 20kV in this example.

Other values such as peak inductor current can be found by substituting values into the appropriate equations from the table above. These can also be used to check the design meets its requirements, before time and money are spent on construction. For example the bang energy of a 80nF capacitor charged to 20kV is 16 Joules. Went multiplied by the maximum break rate of 500, this does indeed give our specified power of 8000 watts.

If there is sufficient interest I might write a small JavaScript program to calculate all of the critical parameters for a DC resonant charging circuit. i.e. You'll enter Pmax, BPSmax and Vdc. The program will do the maths and tell you what components to use to meet your spec.

ADVANTAGES & DISADVANTAGES

The DC resonant charging topology exhibits a number of important differences when compared to the more common AC resonant charging. These are summarised in the lists below:

Advantages:

Eliminates the influence of the supply line frequency on the charging circuit behaviour.

Allows a wide range of firing rates to be investigated with a variable speed rotary spark gap, without encountering beating and surging.

Provides inherent voltage doubling allowing high bang energies to be achieved using a relatively low voltage supply.

Allows power throughput to be controlled by altering the rotary speed.

Eliminates the runaway resonant rise that can occur with the AC resonant charging arrangement. Safety gaps can be dispensed with !

Charging current is zero when the rotary electrodes align so the likelihood of power arcing in the rotary gap is reduced.

Charging is slow immediately after the spark gap fires. This greatly reduces the risk of re-ignition at low rotary speeds.

Power throughput, voltages, and currents can all be predicted with relative ease.

Provides excellent load sharing if a 3 phase rectifier is used at higher powers.

Disadvantages:

More complex circuit is required.

Greater cost,

Large DC smoothing capacitor is needed unless 3-phase power is used. Such a capacitor is expensive, and stores lethal energy.

High voltage, high inductance charging inductor is needed. This is a specialised part and may be difficult to obtain.

Requires a 3-phase supply to be most effective.

Current draw is non-sinusoidal. The line current consists of intense current pulses at the peaks of the AC suply voltage to keep the smoothing capacitor charged. This causes a poor power factor due to waveform distortion.

Information sources

Most of the information for this section was gathered from posts by Greg Leyh and Bert Hickman to the Pupman Tesla list over the last few years. There did not appear to be much in the way of reference material available on the subject of DC resonant charging, so many of the design equations were derived from original circuit theory. The DC resonant charging topology was also familiar to me as a power electronincs engineer, as it often appears in "Soft-Switching" resonant converter designs.

Click here to go back to the previous section about DC resistive charging.

Back to home page