DRIVER CIRCUIT BEHAVIOUR

This is the detail of how to design a good Solid State coil driver. It assumes that you have read the previous section about the load presented by a Tesla coil to the driver.

There are many possible configurations for the solid state driver, but the following sections describe the behaviour of a simple half-bridge switching arrangement feeding the base of a Tesla resonator. In later sections other drive methods and more complex topologies are discussed.

We will start with the simplest analysis using "ideal" components. The circuit is then developed to investigate the effects of real-world components and behaviour under adverse conditions.

Effects of resonant load on the driver at exactly Fres

In practice solid state devices such as MOSFETs or IGBTs are used for the switches T1 and T2 to achieve the required switching speed. The arrow on each switch in the circuit diagram serves as a reminder that these devices usually only control conduction in one direction.

The operation is described step by step below:

On a timing diagram the waveforms look like this:

Although this analysis is simplified slightly, it is very close to the real behaviour of a practical driver circuit, and a few things are worth noting from the results. Notice how the current flowing through the load (and through the switches) passes through zero at the instant when the switches change state. This only happens when the driver is perfectly in tune with the resonator, and has a number of advantages:

1. Greatly reduced switching losses.
   
In other inverter applications there is usually significant current flow through the switches that must be interrupted at the switching instants. Therefore switching losses form a large proportion of the total losses in conventional inverter designs. However, when the load is resonant at the drive frequency there is no current flowing at the switching instant so no power is dissipated during the switching transitions. This reduces heating in the switches.
.
2. Greatly reduced spikes and ringing.
   
There is no abrupt switching of large currents, so the maximum rate of change of current (di/dt) is simply the slope of the sinusoidal load current.
This can be contrasted with hard switched applications where currents of many amps are switched in tens of nanoseconds. (di/dt effects on stray circuit inductances are reduced markedly due to this Zero Current Switching behaviour.)
.
3. Improved load sharing of paralleled switches.

When several switches are paralleled for greater current handling, the load current must be shared evenly between devices. The temperature coefficient of MOSFETs assists static balancing of the load current. However dynamic load sharing can be problematic at high switching frequencies, due to mismatches in the switching speeds of the paralleled devices. In this particular case the current through the switches is near zero for some time around the switching instants, so matching of switching times is less critical. The load current increases slowly at the start of each conduction period so the first devices to turn-on do not get hit with the full load current immediately. Similarly the last devices to turn-off only have to handle the tail of the current as it falls to zero.
.
4. Reduced avalanche stresses for series connected switches.

When switches are series connected for greater voltage handling, avalanching occurs in the last devices to turn on, and the first devices to turn off. Under the conditions being investigated here little current flows through the switches at the switching instant. Therefore the avalanche energy of series connected devices is reduced dramatically. (Although manufacturers now specify avalanche ratings, this mode of operating is stressful to the devices. Series connection of silicon switches can be troublesome and minimising avalanche energy will improve reliability.)
.

Now that we have got excited about how well this simple half-bridge driver would work in an ideal world with ideal components and with perfect tuning, it is time to take a look at what can go wrong in practice !

The requirement for "free-wheel" diodes

Unfortunately real life is never so simple. Two factors act to complicate issues slightly:

1. It is not possible to guarantee that the driver will always be in perfect tune with the Tesla resonator at all times, and under all conditions.

2. In reality it is not possible to open one switch and close the opposing switch at exactly the same instant in time.

The second point is a serious issue since simultaneous conduction of both switches T1 and T2 shorts the supply. This leads to a very high current pulse down the leg of the half-bridge and is very damaging to silicon switches. Such a condition is known as shoot-through (or cross-conduction) and must be eliminated. The shoot-through problem is easily overcome by including a short delay between opening one switch and closing the opposing switch. This delay is called "dead-time" since no switches are conducting, and ensures that both switches cannot be closed simultaneously.

The introduction of the two free-wheel diodes means that there are now 4 possible states in the switching cycle. Not only can the load current be carried by switch T1 or T2, but it can also be carried by diode D1 or D2. Now things get a little more complicated.

The way in which the load current is transferred from one device to another depends on the tuning of the driver with respect to the resonator…

Effects of being "out of tune" on the driver

In earlier sections covering the behaviour of the Tesla coil as a load, we saw that the load current does not necessarily change direction at the same time as the applied voltage. In fact it was found to lead or lag behind the applied voltage depending on the tuning of the driver. This determines the direction of the load current at the instant of the dead-time:

• If the driver is tuned to a frequency above the resonant frequency of the Tesla coil, then the load changes direction after the dead time.
  In this case the free-wheel diodes sustain the load current during the dead time.
  .
• If the driver is accurately tuned to the resonant frequency of the Tesla coil, then the load current will be near zero during the deadtime.
  In this case little current flows through the free-wheel diodes.
  .
• If the driver is tuned to a frequency below the resonant frequency of the Tesla coil, the load current changes direction before the dead time.
  In this case, it is the free-wheel diodes which allow the load current to change direction before the dead-time. (Remember that semiconductor switches can only control conduction in one direction.)
  .

This is of interest to us as it determines how much current flows in each component, and what happens when the load current is passed from one component to another. Most of the stresses that a solid-state driver experiences in this application are a result of large currents being commutated between switches and free-wheel diodes. This can cause over-voltage transients or current surges. Both are undesirable and lead to device failures.

We will now look at what happens in our half-bridge when it is not tuned perfectly to the resonant frequency of the Tesla coil. Let us start by looking at the case which is easiest to analyse…

Effects of resonant load on the driver just above Fres

Steps in the switching cycle,
Voltage and current waveforms,
Free wheel current."
Stray inductance.
ZVS transition.
Forward recovery problems.
Voltage overshoot at device turn-off.

Effects of resonant load on the driver just below Fres

Steps in the switching cycle,
Voltage and current waveforms,
Free-wheel diode behaviour.
Reverse recovery problems.
Isolating the MOSFET body diodes.
Current overshoot at device turn-on.
Effects on current monitoring.

Beware the MOSFET body-diode !

Those familiar with MOSFETs will know that the fabrication process results in a built-in anti-parallel diode between the source and drain terminals of the device. This is often referred to as the "body-diode." Referring to any MOSFET data sheet will reveal specifications for this intrinsic diode.

At first it appears that the internal body-diodes are a bonus since they provide the desired free-wheel diode function for free. This is often the case in many power electronics applications where they provide the function of the free-wheel diodes with ease. Sadly it is not the case in this application. The MOSFET body-diode is a side effect of the fabrication process and is not a particularly good diode. The same design criteria for good MOSFET characteristics do not produce the best body-diode characteristics. The design of a MOSFET is always a compromise, and it is the characteristics of the body-diode that suffer.

When compared to discrete high speed diodes, the body-diode's reverse recovery time is very long. This means that the diode takes a long time to turn off when the current flowing through it changes direction. As explained previously, this leads to a shoot-through condition when the opposing switch is turned-on. For this reason the body-diodes are clearly not suitable for free-wheel diode duty in this application and should be isolated.

The use of external free-wheel diodes gives the designer greater choice in the characteristics of this critical component. It also removes a source of dissipation from the MOSFETs, since the free-wheel current no longer enters onto the MOSFET die.

Although dedicated fast-recovery diodes are much faster than the MOSFET body-diodes, they still have a finite reverse recovery time. This is typically several tens of nanoseconds. Any remaining reverse-recovery problems can usually be solved by slowing down the turn-on of the switches. This allows longer for the free-wheel diodes to recover, and reduces the peak reverse recovery current. (The recovery is also softer and results in less radiated interference too!)

Beware excessive dead-time !

The amount of dead-time between opening one switch and closing the opposing switch should be just sufficient to prevent simultaneous conduction of both switches, and no longer.

Higher currents conducted for longer periods lead to higher dissipation in the free-wheel diodes. However, more importantly, the harder the free-wheel diodes are driven into forward conduction, the harder they are to turn off. (The reverse recovery time becomes longer.)

For this reason the driver should be accurately tuned to minimise the current flow during the deadtime, and the dead-time should be kept short to minimise diode conduction time.

Snubbers

Over-voltage snubbing,
Over-current snubbing,
Damping of parasitic resonances,
Snubber energy,
Snubber effectiveness,
Lossless snubbing and ZVS transition,
Diode clamping loop,

Resonator impedance

Components of resistance.
DC resistance.
Skin effect.
Ground plane losses.
Radiation resistance.
Proximity effect.
Impedance changes due to spark loading.
Reflected load theory.
Impedance inversion.
The constant current sink model.
Resonator detuning.
Frequency tracking (dynamic tuning).

Drive methods

Base feed method.

This is the drive method that has been discussed in all of the previous sections and is by-far the simplest arrangement. The base of the resonator is connected directly to the output of the inverter with a single wire. The return current is capacitively coupled to the surroundings and ultimately back to ground. The base-fed resonator is modelled as a series resonant LCR circuit, and its behaviour has already been described in considerable detail.

In practice the base feed method does not give good results unless a relatively high drive voltage is used. This is because the base impedance at resonance can still be tens or hundreds of ohms, and rises further during spark breakout. Therefore the resonator does not draw much current unless a voltage of several hundreds or thousands of volts is used.

The following list summarises some of the properties of the base-feed approach:

(The author knows of one individual who has obtained excellent spark performance from a base-fed solid state Tesla coil. However, his design uses a supply voltage of 1500 volts, in order to force many kilowatts of power into the resonator. This approach appears relatively simple on the surface, although the construction of a robust, high power, high frequency inverter to operate from a 1.5kv supply is not for the beginner !)

For this reason one of the methods described later can be used to provide a better impedance match between the low impedance of the driver and the medium-to-high impedance of the Tesla resonator. This allows the driver to operate from a lower supply voltage such as a battery, or directly from the AC mains.

Primary coil drive method.

This analysis shows us that the series resonant nature of the Tesla coil is reflected back to the primary due to the magnetic coupling between the coils. The series resonant LCR model of the secondary appears as if it were actually connected in parallel across the primary winding, although its impedances are transformed down due to the turns-ratio between the two coils.

From the last schematic above, we can see that the load current (Iload) supplied by the driver is now the sum of two components. These are Imag and Ires. We will consider the significance of each of these components below:

Effect of changing k

As the degree of coupling is increased, two things happen:

1. More of the secondary winding is coupled to the primary so Ls1 increases. This increases the voltage gain due to transformer action. The turns ratio effectively increases because the primary sees a greater number of the secondary turns.)

2. Less of the secondary winding is left free to resonate with Cs. This decrease in the remaining resonant inductance Ls2 causes the resonant frequency to rise as the coupling is increased !

This behaviour is summarised in the drive impedance plot shown below:

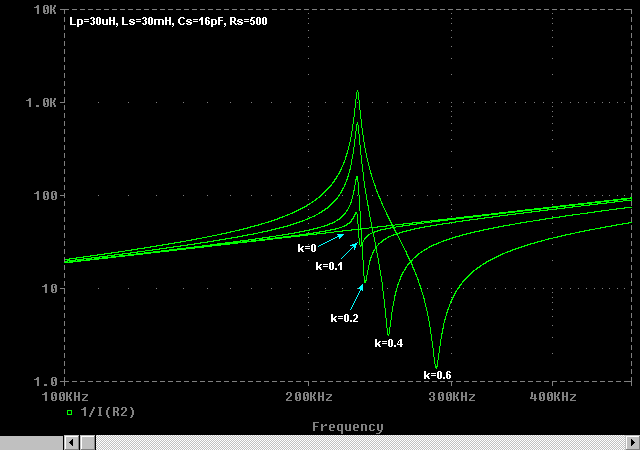
Graph showing typical variation in primary impedance with different degrees of coupling.

Notice how all of the lines lie around the same straight line labelled k=0. This is the impedance of the primary coil on its own, with no coupling to the seconadry. The impedance plot begins to deviate from this straight line as the coupling is increased and the primary begins to "see" more of the resonator.

The points of interest on this graph are the impedance minima. The minimum point for each line represents the frequency at which maximum current is drawn from the driver and the resonant component Ires is in phase with the applied voltage. This is also the point which gives the maximum voltage gain at the top of the resonator, and therefore best spark performance.

Notice that the resonant frequency with minimum primary impedance changes as the coupling is varied. This is because more of the resonator is coupled to the primary as k is increased, leaving less of the secondary coil free to resonate.

The resonant part of the secondary was earlier found to be: Ls2 = (1 - k²) Ls
Since frequency is proportional to 1 / sqrt (L C) then it can be shown that the resonant frequency seen at the primary is equal to the free-standing (un-coupled) resonant frequency of the secondary multiplied by the following factor:

If k=0, the resonant frequency is equal to the natural resonant frequency of the resonator, but there is no coupling. We effectively have two separate circuits. As k is increased towards unity, Ls2 decreases to zero, and the resonant frequency seen at the primary heads towards infinity! At k=1 we basically have a conventional transformer with no resonant behaviour.

This shows that it is important to remember to re-tune after adjusting the coupling when using a solid state driver and a primary coil to drive the resonator!

Note: An impedance maximum point also exists in the frequency response above. This is because the reflected resonator impedance is slightly capacitive at this frequency and it cancels out the inductive reactance of the primary coil. At this frequency a parallel resonant circuit is formed between the primary inductance and the net capacitive reactance reflected back from the secondary. It is of little practical importance to us since it represents a high impedance to the driver. Therefore it draws negligible current from the driver. It is mentioned here for completeness.

Effect of changing primary inductance Lp

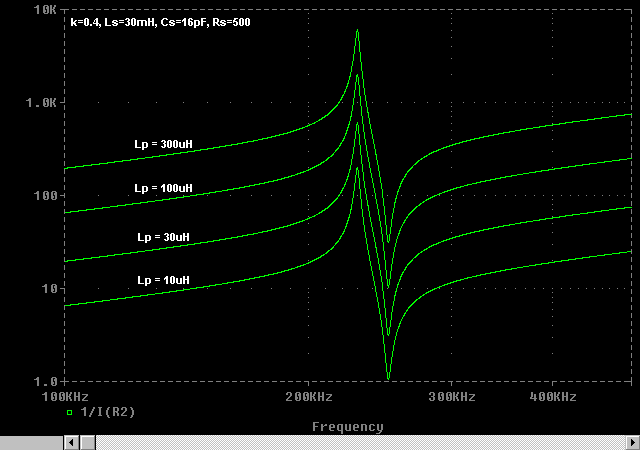
Graph showing typical variation in primary impedance with different numbers of primary turns.

Notice how increasing or decreasing the primary inductance (Lp) effects the whole primary impedance in the same way. Both the magnetising current and the resonator current components change as a direction function of Lp. However, the positions of the resonant peaks are not changed provided the coupling remains constant. Altering Lp provides an easy way to increase or decrease the total load current without changing the resonant frequency.

For example, halving the number of primary turns reduces the primary inductance to approximately one quarter of its previous value. In an ideal world the impedance presented to the driver would reduce to one quarter of its previous value and there would be a corresponding increase in the current drawn from the driver.

Note: In practice the impedance does not fall quite as far as one quarter of its previous value. Therefore the current does not quite quadruple. We will see later that this is due to a strange "negative resistance" property of the spark discharge from the top of the coil, when we attempt to drive more power into it!

Summary on effects of Lp and k.

The choice of Lp and k are very important. In fact I think that one of the main challenges in solid state Tesla coil work is in juggling these two parameters to get maximum power transfer into the resonator.

If Lp is too small, the magnetising current becomes unacceptably high. Although this does not contribute to the supply current of the driver, it does contribute to heating in the switches. It also increases the current ripple seen by the supply reservoir capacitors.

If Lp is too great, then there is little step-up due to transformer action. As a result, the Tesla resonator is not well matched to the driver, and little power is drawn from the driver.

If k is too small, then the load current is dominated by the magnetising current, and little of the current supplied by the driver actually contributes to resonance in the secondary winding.

If k is too great, then there is a risk of electrical flashover. This is due to the close proximity demanded to achieve this degree of pri-sec coupling, and the large sparks that result !

It is my opinion that Lp should be made only sufficiently large to obtain an acceptable magnetising current, then k should be maximised as far as possible to get the minimum possible load impedance at resonance. This is presently my recipe for effective power transfer using this particular drive method. Good power transfer can only be achieved with reduced coupling if the drive voltage is increased. Consider that there is less "step-up" due to transformer action as the coupling is reduced. Therefore you have to drive the primary with a correspondingly higher voltage to make up for this, and acheive the same performance.

The author's present solid state Tesla coil system makes use of a 18 turn 20uH primary inductor driven with +/- 340v at 350kHz. This is tightly coupled to the secondary winding with a coupling coefficient of approximately 0.55. This provides good power throughput, with an acceptably low magnetising current. However, such a high coupling coefficient demands close positioning of the primary and secondary, and tends to promote flashovers. The distance between the primary and secondary windings is less than half of an inch, and sparks of 18" are common from the toroid, so insulating between the two coils is a challange.

One may think that such a high coupling coefficient produces most of the voltage gain by transformer action, and little voltage rise due to resonance in the un-coupled portion of the secondary. This is actually true, but we must realise that spark breakout loads the secondary winding ruining the Q, so resonant rise is not good after spark breakout. The base impedance of a physically small resonator seems relatively high to start with, and this increases further following spark breakout, therefore a high coupling coefficient is required to obtain maximum transformer action, and achieve good matching under sparking conditions.

Transformer feed method, (The magnifier arrangement.)
Resonant primary circuit.
Bipolar coil driver.
Frequency tracking methods.
The power oscillator.

Back to home page