Abstract

This paper discusses many of the factors that influence the design of a solid state resonant coil driver. It assumes that the reader has basic knowledge of circuit theory and is primarily aimed at those with some experience in the field of power electronics. Simple circuit theory is used to analyse the nature of the load presented by a Tesla coil. This model is then used to investigate implications on the design of the drive electronics. Finally the operation of the drive electronics is explored under a variety of operating conditions. This paper attempts to concentrate more on conclusions and their implications, rather than getting bogged down in complex maths and circuit theory. It aims to highlight the shortfalls in classical inverter designs when being applied to this unusual application.

Introduction

When designing a Solid State Tesla Coil driver, the designer can consult many power electronics books, technical papers, and manufacturers data sheets. These often highlight good design practice, and may include valuable tips for layout and construction. However, the designer should be aware that the solid state Tesla coil driver has a distinct difference when compared to most classical inverter designs. This difference is in the nature of the load, and is worth looking at in some detail since it can make the difference between a robust design that performs well, and one that fails prematurely.

With the exception of some modern "soft-switching" schemes, this resonant load condition is not discussed in many power electronics books. However, it is worth looking into the nature of the resonant load in more detail. After all, we seek to maximise the power that we can deliver to this resonant load, whilst also ensuring that our inverter will have a long and happy life driving this load. Building an inverter based on traditional power electronics theory does not necessarily ensure either of these requirements are met.

The sections that follow describe the nature of the load that a Tesla coil resonator presents to the driver under various conditions, and the implications that this has on the design of the driver circuit. Some thought is also given to the effects of spark breakout and various drive methods for coupling power into the coil effectively.

The behaviour of the load

Such a high-Q resonant load as that presented by a Tesla coil is rarely encountered in either the power electronics or RF engineering fields. High Q-resonators essentially store up energy over time. This is the exact opposite of most power supply and RF systems where the aim is to transfer power quickly with the minimum of losses. (The storing-up of energy in a high-Q resonator implies high circulating currents and therefore increased losses, which are usually undesirable.) However, in our application it is this "ring-up" over several cycles that gives rise to the high output voltages and sparks that we desire.

The load presented by the Tesla coil, when fed from its base, can be modelled as a Resistance R in series with inductive Xl and capacitive Xc components. This is familiar as the series RLC circuit shown below:

Since all three elements are connected in series, then the total impedance presented to the driver is the sum of the three components.

Note that real power can only be dissipated in R, since Xl and Xc are purely reactive.

(Please do not get deterred from reading this because of the algebra. You do not need to understand all of the maths to understand this paper. I have tried to keep the maths to an absolute minimum !)

Driving the coil at exactly Fres

At a particular frequency the values of the inductive reactance Xl and capacitive reactance Xc are equal and opposite. This is known as the resonant frequency and can be found as follows:

Some rearranging to find f confirms that the resonant frequency depends on the values of L and C as expected.

Fres = 1 / 2 pi sqrt (L C)

Since the reactances Xl and Xc are equal and opposite when the coil is driven at Fres, they cancel each other out and the load impedance appears like a pure resistance.

Zload = R + j Xl + j Xc

Zload = R

There are three important consequences of this:

1. The impedance Zload at resonance is the lowest impedance that the Tesla coil can ever present to the driver. Therefore the coil will draw maximum current from the driver when driven at Fres. The impedance is always higher at any other operating frequency due to the addition of the reactive components.
   .
2. If maximum current flows through the load at the resonant frequency, then application of Ohm's law shows that maximum voltage must also be developed when driven at Fres.
   .
3. The pure resistive load at resonance implies no phase shifts. It is reactive components that give rise to phase shifts and since these cancel at Fres then the load current drawn from the driver must be in phase with the applied voltage.
   .

The resonator presents a very well behaved load to the driver provided it is driven at exactly the correct resonant frequency. However, this is difficult to ensure under all conditions. Therefore we should look at what happens if we drive the resonator at a frequency that deviates significantly from its natural resonant frequency.

So how much does the driver frequency need to deviate from the resonant frequency before something interesting happens…?

Q factor and bandwidth

In the case of a Tesla coil resonator we usually seek to minimise the winding resistance, and hence maximise the unloaded Q factor of the resonator. This keeps power dissipation due to I²R losses to a minimum, and also maximises the voltage gain that we get due to resonant rise.

Q = Xl / R

For a given inductance and operating frequency, Xl remains fixed, so maximising Q implies minimising R.
Since the load impedance equals R at resonance, this also ensures that the resonator presents a nice low impedance to the driver at resonance.

In order to see the effect of driving the resonator at frequencies above and below its natural resonant frequency, we need to look at the formula for the load impedance again because Xl and Xc will no longer cancel each other out:

The Xl term is proportional to the applied frequency, and the Xc term is inversely proportional to the applied frequency. (The resistive part R is just plain old R regardless of the frequency.)

As we move away from the natural resonant frequency, Xl and Xc will no longer cancel each other out, and we have a small net reactive contribution. Minimising R has the side effect that it makes even small amounts of Xl or Xc become a significant part of the total load impedance.
(EE's will draw some vector diagrams at this point, just to be sure ;-)

In summary the load impedance becomes very sensitive to the smallest of changes in f around the natural resonant frequency.

Driving the coil well away from Fres

We can quickly see that driving the coil at a very high frequency, (for example f = Infinity,) would cause the inductive reactance Xl to be very large and the inductive reactance Xc to be insignificant. In this case the load impedance would be very high because it is dominated by the large jXl component. Also, because the jXl term is very large, it swamps the resistive part R and the load is considered to be highly reactive.
At frequencies far above the natural resonant frequency of the coil, the load appears almost like a pure inductor. There is a 90 degree lag between the applied voltage and the current that flows through the load.

Similarly, if we consider driving the coil at a very low frequency, (for example f = 0 Hz,) then we can see that the opposite situation occurs. The capacitive reactance Xc becomes very large and the inductive reactance Xl becomes insignificant. In this case the load impedance is very high because it is dominated by the large jXc component. Also, because the jXc term is very large, it swamps the resistive part R and the load is highly reactive again.
At frequencies far below the natural resonant frequency of the coil, the load appears almost like a pure capacitor. The current that flows in the load leads the applied voltage by 90 degrees.

Since both of these situations result in a high load impedance then little current flows. Therefore there is minimal danger to the driver circuit when it is tuned a long way from the resonant frequency of the Tesla coil.

If driving the Tesla coil at the exact resonant frequency results in a pure resistive load, and driving the resonator far away from resonance results in a high impedance (open circuit) condition, then what happens at frequencies in-between ?

Problems associated with being "out-of-tune" are most troublesome when the inverter attempts to drive the resonator at a frequency that is only slightly away from the natural resonant frequency of the coil. This is very important when you consider that the small bandwidth of a high Q resonator demands very precise tuning : A difficult thing to guarantee in practice given the influence of corona loading and the surrounding environment !

Driving the coil just above Fres

If we consider a resonator being driven at a frequency f just above its natural resonant frequency, we can see that there will be a small net inductive reactance. This net reactance is small compared to the resistive part of the load, so the total magnitude of Zload is still low and considerable current flows. However, there is enough inductive reactance to cause a significant phase shift in the current that flows through the load.

When driven at the exact resonant frequency, we saw that the load current was sinusoidal and was precisely in phase with the applied voltage waveform. This is no longer the case when the coil is driven slightly above its resonant frequency. A substantial current still flows, but the current drawn by the load starts to lag behind the applied voltage waveform by a short time as shown below:

This has some implications on the design of the inverter if it is to withstand this condition without damage. (See DRIVER CIRCUIT BEHAVIOUR sections later.)

Driving the coil just below Fres

If we consider a resonator being driven at a frequency f just below its natural resonant frequency, we can see that there will be a small net capacitive reactance. This reactance is small compared to the resistive part of the load, so the total magnitude of Zload is still low and considerable current flows. However, there is enough capacitive reactance to cause a significant phase shift in the current that flows through the load.

When driven at the exact resonant frequency, we saw that the load current was sinusoidal and was precisely in phase with the applied voltage waveform. This is no longer the case when the resonator is driven slightly below its resonant frequency. A substantial current still flows, but the current drawn by the load starts to lead the applied voltage by a short time as shown below:

This property of load current reversal before the applied voltage is somewhat unique and is a direct consequence of charge storage in the capacitance of the Tesla coil. Most inverters for motor drives or power supply applications drive power into loads which are highly inductive. For this reason the behaviour discussed here is rarely encountered elsewhere in the Power Electronics field.

This strange behaviour has some important implications on the design of the driver. Specifically it must be able to withstand this leading power factor condition without damage. (See DRIVER CIRCUIT BEHAVIOUR sections later.)

Impedance plot

The impedance plot below summarises how the impedance of a base-fed Tesla resonator changes with tuning. It shows how the magnitude of the load impedance varies as the frequency of the driver is swept from very low to very high.

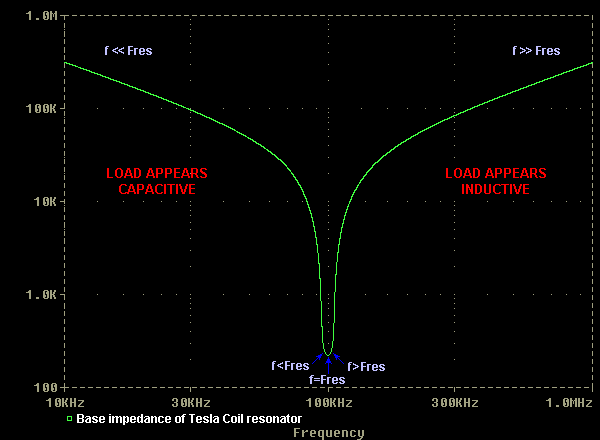
Either side of the resonant frequency the impedance presented at the base of the coil is very high and little current is drawn. Close to the resonant frequency the impedance presented to the driver is low and considerable current is drawn. The width and depth of the "impedance dip" depend on the Q factor of the resonant circuit.

Higher Q-factors are desirable because they result in maximum voltage gain at the top of the resonator. They also produces a narrow impedance dip which is very deep. This characteristic offers good loading of the driver provided it can be accurately tuned to the resonant frequency of the coil.

The plot below shows the current drawn (top trace,) and the phase of this current relative to the applied voltage over the same range of frequencies.

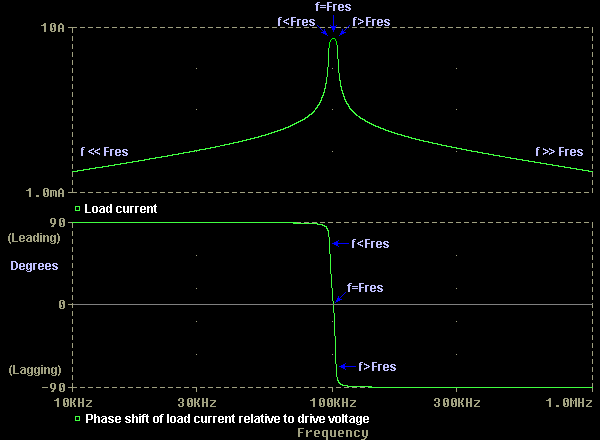
Notice how considerable current flows for a narrow band of frequencies around the resonant frequency of the coil. Also notice that the phase of the current is shifted dramatically for small deviations either side of the resonant frequency. It is this phase shift that is the cause of many headaches in solid state coiling.

Higher resonant modes

At this point it should be mentioned that a practical Tesla resonator exhibits other resonant modes in addition to the "quarter wave" or fundamental mode that we have discussed so far. In this respect it behaves much like a transmission line or guitar string. The 1/4 wave mode that we have investigated represents the lowest frequency peak in the response of the resonator, and results in a single voltage maxima at the end of the resonator. Driving the resonator at this fundamental frequency is most useful to us since we desire maximum voltage rise at the top of the resonator only. We can also conveniently model it as a series RLC circuit.

When driven at approximately twice this frequency the Tesla resonator develops a voltage maxima at the centre of its length and a minima at the far end. This is known as the "half wave" mode. It is not of great use to us since maximum voltage is developed part way along the length of the coil.

When driven at higher frequencies still, the resonator displays a number of smaller voltage maxima and minima distributed along its length. These resonant peaks occur at approximate multiples of the fundamental frequency. However, we should resist the temptation to call them harmonics. They are not true harmonics since they do not appear at exact multiples of the fundamental frequency.

These higher resonant modes are of little interest to us since we drive our coil at the fundamental frequency, but a plot is shown below for completeness. The graph shows how the base impedance of a resonator varies over a wide frequency range. Therefore the dips in the graph represent the frequencies at which the impedance is minimum. Maximum current will be drawn from the driver at these resonant frequencies.

(The data for this plot was kindly provided by Paul Nicholson.)

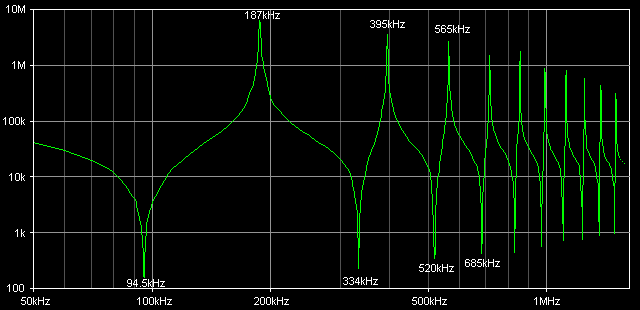
Note: Although we often drive our resonators from a square wave voltage source which is rich in odd harmonics, the current drawn by the resonator is sinusoidal as it responds to the fundamental frequency mostly. The harmonics of the squarewave do not appear to excite higher resonant modes present in the resonator. This is thought to be due to the fact that the higher modes of the resonator do not occur at exact multiples of the driver frequency.

Consider the data in the graph above. The quarter wave resonant frequency of the Tesla coil is 94.5kHz. If this is driven from a squarewave voltage source at 94.5kHz then the most dominant harmonic of the drive waveform is the 3rd harmonic at 283.5kHz. This is some distance away from the 3/4 wave resonant mode of the Tesla coil at 334kHz. Therefore little current is drawn from the driver at its 3rd harmonic frequency. The next most dominant harmonic of the drive signal is the 5th harmonic at 472.5kHz. However, this is even further from the coil's 5/4 resonant mode at 520kHz.

For a squarewave drive, only odd harmonics are present, and the amplitudes of these harmonics diminish in proporion to 1/f. Therefore it is unlikely that any high order harmonic that happens to coincide with a high order resonant mode would result in significant current flow at that frequency. For this reason we will only concern ourselves with the 1/4 wave mode for most of the following discussions. It will be modelled using a simple series resonant RLC circuit.

Now we have a good understanding of the behaviour of the Tesla coil as a load when driven at frequencies around its natural resonant frequency. We will go on to look at the implications that this has on the drive electronics, and then how to design a driver that satisfies these criteria.

Click here for the next section on DRIVER CIRCUIT BEHAVIOUR.

Back to home page